[3분논문] 제22회 - 자이로이드 광자결정에 생기는 웨일점과 선마디

황용섭의 3분논문 제22회입니다.

총시간은 7분 54초입니다.

재미있게 들어보세요.

# 방송 바로 듣기

1. 001.mp3

# 방송 mp3 파일 내려받기

(여기를 눌러주세요)

(참고: mp3 파일은 예고 없이 삭제될 수 있습니다.)

팟캐스트 검색: "3분논문"

팟캐스트 주소: http://itunes.apple.com/us/podcast/3bunnonmun/id568397433

RSS 피드: http://www.iblug.com/xml/itunes/3minpaper.xml

# 논문표지

# 간단한 정보

글쓴이: Ling Lu, Liang Fu, John D. Joannopoulos and Marin Soljačić

제목: Weyl points and line nodes in gyroid photonic crystals

학술지: Nature Photonics

발행년월: 2013년 3월

이어가기: http://dx.doi.org/10.1038/nphoton.2013.42

# 용어

- Weyl point: 그래핀에서 나타나는 Dirac point를 3차원으로 확장한 것.

- gyroid: 자이로이드. 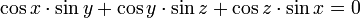 의 수식으로 표현된다.

# 발췌

1. 

... the ease of its eventual experimental realization and the associated characterized of the Weyl points.

2.

2D Dirac cones are not robust ... In contrast, 3D Weyl points are topologically protected gapless dispersions robust against any perturbation.

# 그림

Figure 1: Real-space unit cell and reciprocal-space Brillouin zone of the gyroid photonic crystals.

a, Real-space geometry in a bcc unit cell where  ,  and  . The two identical gyroid structures in red and blue are high-refractive-index (n = 4) materials; they are inversion pairs with respect to the origin (o). The illustrated air-sphere of radius r (r/a = 0.13) located at is only placed there when structural symmetry needs to be broken. b, The bulk and (101) surface Brillouin zones of the bcc lattice. Weyl points and line nodes investigated in this work lie in the green (101) plane through the origin (Γ) of the bulk Brillouin zone, projecting onto the (101) surface Brillouin zone. Γ-N is along  and Γ-H is along [010] (ŷ). c, An air-isolated DG surface can be formed by terminating the perturbed gyroid (red) but not the other (blue). The SG photonic crystal on top has a large complete bandgap, as shown in Fig. 2a.

Figure 2: Gapless photonic band structures of the DG photonic crystals.

a–d, Band structures without (a) and with (b–d) perturbations. All the dispersion behaviours close to the degeneracy points in this figure can be described well by the low-energy theory model in Supplementary Section SB. Because P and T are not broken at the same time in these photonic crystals, k and −k are degenerate in the band structures. A few lowest-value contours of the frequency difference between the fourth and fifth bands are shown (hexagonal insets) for each band structure in the (101) plane. The contour spacing is 0.004 in normalized frequency, and ‘ + ’ and ‘−’ are used to label the chiralities of the Weyl points. a, The original DG photonic-crystal band structure has a threefold degeneracy at Γ among the third, fourth and fifth bands in a pseudo-gap. The SG photonic crystal has a huge frequency gap covering the pseudo-gap frequency region. b, We place the two air-spheres on the two gyroids: one air-sphere (r/a = 0.07) is located at , the other is its inversion symmetric counterpart. Under this perturbation, the fourth and fifth bands touch linearly in a closed line around Γ in the (101) plane. The linear crossing line is highlighted by a green stripe; this structure does not yet exhibit any Weyl points. c, We apply a P-breaking perturbation by placing one air-sphere (r/a = 0.10) in one of the gyroids, but not the other. Two pairs of Weyl points appear (highlighted by green circles): one pair appears along Γ-H and the other along Γ-N. d, We apply a T-breaking perturbation (P conserved) by applying a d.c. magnetic field (dimensionless |B| = 0.875) to the DG photonic crystal without air-spheres. Only one pair of Weyl points appears (highlighed by the green circle), along the direction of the magnetic field (Γ-N).

# 결론

2차원 디락점에 해당하는 3차원 웨일점이라는 개념을 광자결정의 구조를 설계하여 구현한 재미있는 논문이다. 계산논문이지만 실험적인 면도 고려하였다. 

끝.

2013년 3월 25일