| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- Monica Hwang
- 예랑이
- english writing
- 3분논문
- 그림
- 자작동화
- 책
- Book
- Yerang Monica Hwang
- 황예랑
- ielts writing
- Subclass 189
- melbourne
- 제주여행
- Skilled Independent visa (subclass 189)
- 호주 이민
- 호주
- IELTS
- Book Review
- 호주 영주권
- australia
- 황평화
- 멜버른
- 평화
- Rosie Banks
- SF
- Skilled Independent Migration
- General training module
- 독립기술이민
- Secret Kingdom
- Today
- Total
꾸로네
[3분논문] 제22회 - 자이로이드 광자결정에 생기는 웨일점과 선마디 본문
황용섭의 3분논문 제22회입니다.
총시간은 7분 54초입니다.
재미있게 들어보세요.
# 방송 바로 듣기
# 방송 mp3 파일 내려받기
(참고: mp3 파일은 예고 없이 삭제될 수 있습니다.)
팟캐스트 검색: "3분논문"
팟캐스트 주소: http://itunes.apple.com/us/podcast/3bunnonmun/id568397433
# 논문표지
# 간단한 정보
글쓴이: Ling Lu, Liang Fu, John D. Joannopoulos and Marin Soljačić
제목: Weyl points and line nodes in gyroid photonic crystals
발행년월: 2013년 3월
# 용어
- Weyl point: 그래핀에서 나타나는 Dirac point를 3차원으로 확장한 것.
- gyroid: 자이로이드. 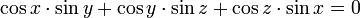 의 수식으로 표현된다.
의 수식으로 표현된다.
# 발췌
1.
... the ease of its eventual experimental realization and the associated characterized of the Weyl points.
2.
2D Dirac cones are not robust ... In contrast, 3D Weyl points are topologically protected gapless dispersions robust against any perturbation.
Figure 1: Real-space unit cell and reciprocal-space Brillouin zone of the gyroid photonic crystals.
a, Real-space geometry in a bcc unit cell where  ,
,  and
and  . The two identical gyroid structures in red and blue are high-refractive-index (n = 4) materials; they are inversion pairs with respect to the origin (o). The illustrated air-sphere of radius r (r/a = 0.13) located at
. The two identical gyroid structures in red and blue are high-refractive-index (n = 4) materials; they are inversion pairs with respect to the origin (o). The illustrated air-sphere of radius r (r/a = 0.13) located at is only placed there when structural symmetry needs to be broken. b, The bulk and (101) surface Brillouin zones of the bcc lattice. Weyl points and line nodes investigated in this work lie in the green (101) plane through the origin (Γ) of the bulk Brillouin zone, projecting onto the (101) surface Brillouin zone. Γ-N is along
is only placed there when structural symmetry needs to be broken. b, The bulk and (101) surface Brillouin zones of the bcc lattice. Weyl points and line nodes investigated in this work lie in the green (101) plane through the origin (Γ) of the bulk Brillouin zone, projecting onto the (101) surface Brillouin zone. Γ-N is along  and Γ-H is along [010] (ŷ). c, An air-isolated DG surface can be formed by terminating the perturbed gyroid (red) but not the other (blue). The SG photonic crystal on top has a large complete bandgap, as shown in Fig. 2a.
and Γ-H is along [010] (ŷ). c, An air-isolated DG surface can be formed by terminating the perturbed gyroid (red) but not the other (blue). The SG photonic crystal on top has a large complete bandgap, as shown in Fig. 2a.
 , the other is its inversion symmetric counterpart. Under this perturbation, the fourth and fifth bands touch linearly in a closed line around Γ in the (101) plane. The linear crossing line is highlighted by a green stripe; this structure does not yet exhibit any Weyl points. c, We apply a P-breaking perturbation by placing one air-sphere (r/a = 0.10) in one of the gyroids, but not the other. Two pairs of Weyl points appear (highlighted by green circles): one pair appears along Γ-H and the other along Γ-N. d, We apply a T-breaking perturbation (P conserved) by applying a d.c. magnetic field (dimensionless |B| = 0.875) to the DG photonic crystal without air-spheres. Only one pair of Weyl points appears (highlighed by the green circle), along the direction of the magnetic field (Γ-N).
, the other is its inversion symmetric counterpart. Under this perturbation, the fourth and fifth bands touch linearly in a closed line around Γ in the (101) plane. The linear crossing line is highlighted by a green stripe; this structure does not yet exhibit any Weyl points. c, We apply a P-breaking perturbation by placing one air-sphere (r/a = 0.10) in one of the gyroids, but not the other. Two pairs of Weyl points appear (highlighted by green circles): one pair appears along Γ-H and the other along Γ-N. d, We apply a T-breaking perturbation (P conserved) by applying a d.c. magnetic field (dimensionless |B| = 0.875) to the DG photonic crystal without air-spheres. Only one pair of Weyl points appears (highlighed by the green circle), along the direction of the magnetic field (Γ-N).# 결론
2차원 디락점에 해당하는 3차원 웨일점이라는 개념을 광자결정의 구조를 설계하여 구현한 재미있는 논문이다. 계산논문이지만 실험적인 면도 고려하였다.
끝.
2013년 3월 25일
'연구자료 > 논문 살펴보기' 카테고리의 다른 글
| [3분논문] 제24회 - 실리콘 나노선 플라즈몬 도파로 (6) | 2013.04.09 |
|---|---|
| [3분논문] 제23회 - 발광 실리콘 나노선 (0) | 2013.04.03 |
| [3분논문] 제21회 - 자기기반 메타분자의 파노공진 (2) | 2013.02.08 |
| [3분논문] 제20회 - 이미징을 위한 메타물질 조리개 (0) | 2013.01.29 |
| [3분논문] 제19회 - 나노포토닉 위상조절배열 (0) | 2013.01.19 |







